Un número es una entidad abstracta que representa una cantidad.
El símbolo de un número recibe el nombre de numeral.
Una entidad es todo aquello que puede percibirse por los sentidos o por la mente, o tambien, lo que puede diferenciarse de su entorno.
Cantidad es todo aquello que puede ser medido o contado.
Del latín adj. numeralis. Palabra, símbolo o grupo de símbolos que representan a un número
{1,2,3, ..., i,ii,iii, ... 01,10, 11, ...} son numerales que se asocian a números {uno, dos, tres, ...}
Tipos de números
Los números más conocidos son los números naturales 0, 1, 2,3,4,5,6,7,8,9 ..., que se usan para contar.
Si añadimos los números negativos obtenemos los enteros.
Fracciones (Cocientes) de enteros generan los números racionales.
Agregando todos los números que son expresables con decimales pero no con fracciones de enteros, obtenemos los números reales;
Si a éstos les añadimos las soluciones (raíces) de los polinomios, llamados números complejos, tendremos todos los números necesarios para resolver cualquier ecuación algebraica.
Tenemos tambien los infinitos y los transfinitos.
Entre los reales, existen números que no son soluciones de una ecuación polinomial o algebráica. Reciben el nombre de transcendentales. El ejemplo más famoso de estos números es π (Pi),
otro ejemplo fundamental e igual de importante es e, base de los logaritmos naturales.
e = 2,71828182845904 . . .
Estos dos números están relacionados entre sí por la identidad de Euler, también llamada la fórmula más importante del mundo.
Existe toda una teoría de los números. Se distinguen distintos tipos de números:
- Números naturales
- Números enteros
- Números racionales
- Números reales
- Números complejos
- Números fundamentales: π y e
Número natural
Un número natural es cualquiera de los números: 0, 1, 2, 3... que se pueden usar para contar los elementos de un conjunto. Reciben ese nombre porque fueron los primeros que utilizó el ser humano para contar objetos de la naturaleza.
Algunos matemáticos (especialmente los de Teoría de Números) prefieren no reconocer el cero como un número natural, mientras que otros, especialmente los de Teoría de conjuntos, Lógica e Informática, tienen la postura opuesta.
Número primo
El conjunto de los números primos es un subconjunto de los números naturales que engloba a todos los elementos de este conjunto que son divisibles exactamente tan sólo por sí mismos y por la unidad (por convención, el 1 no se considera primo). Los veinte primeros números primos son: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67 y 71.
Nótese el hecho de que todos los números naturales son divisibles por sí mismos y por la unidad.
El teorema fundamental de la Aritmética establece que cualquier entero positivo puede representarse siempre como un producto de números primos, y esta representación (factorización) es única.
Número entero
Los números enteros son una generalización del conjunto de números naturales que incluye números negativos (resultados de restar a un número natural otro mayor además del cero). Así los números enteros están formados por un conjunto de enteros positivos que podemos interpretar como los números naturales convencionales, el cero, y un conjunto enteros negativos que son los opuestos de los naturales (éstos pueden ser interpretados como el resultado de restar a 0 un número natural).
Estructura de los números enteros
Los enteros con la adición y la multiplicación forman una estructura algebraica llamada anillo. Pueden ser considerados una extensión de los números naturales y un subconjunto de los números racionales (fracciones). Los números enteros son subconjunto de los números racionales o fracciones, puesto que cada número entero puede ser considerado como una fracción cuyo denominador es el número uno.
Los números enteros pueden ser sumados y restados, multiplicados y comparados. Si la división es exacta, también pueden dividirse dentro del mismo conjunto de los enteros. La razón principal para introducir los números negativos sobre los números naturales es la posibilidad de resolver ecuaciones del tipo:
- a + x = b
para la incognita x.
Matemáticamente, el conjunto de los números enteros con las operaciones de suma y multiplicación, (ℤ,+,·) constituye un anillo conmutativo y unitario. Por otro lado, es un conjunto completamente ordenado sin cota superior o inferior: los enteros no tienen principio ni fin. El conjunto de los números enteros se representa mediante  (el origen del uso de Z es el alemán Zahlen 'números').
(el origen del uso de Z es el alemán Zahlen 'números').
Número racional
En sentido amplio se llama número racional o fracción común a todo número que puede representarse como el cociente de dos enteros con denominador distinto de cero; el término "racional" alude a "ración" o parte de un todo, y no al pensamiento o actitud racional, para no confundir este término con un atributo del pensamiento humano.
En sentido estricto, número racional es el conjunto de todas las fracciones equivalentes a una dada. De todas ellas se toma como representante canónico del número racional en cuestión a la fracción irreducible, la de términos más sencillos. Las fracciones equivalentes entre sí -número racional- son una clase de equivalencia, resultado de la aplicación de una relación de equivalencia al conjunto de números fraccionarios.
El número racional permite resolver ecuaciones del tipo ax = b cuando a y b son números enteros.
El conjunto de los racionales se denota por  , que significa quotient, "cociente" en varios idiomas europeos. Este conjunto de números incluye a los números enteros y es un subconjunto de los números reales.
, que significa quotient, "cociente" en varios idiomas europeos. Este conjunto de números incluye a los números enteros y es un subconjunto de los números reales.
Los números racionales cumplen la propiedad arquimediana o de densidad, esto es, para cualquier pareja de números racionales existe otro número racional situado entre ellos, propiedad que no estaba presente en los números enteros, por lo que los números racionales son densos en la recta de los números reales.
- Consideremos las parejas de números enteros
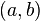 donde
donde 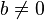 .
.  denota a
denota a 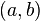 . A a se le llama numerador y a b se le llama denominador
. A a se le llama numerador y a b se le llama denominador- Al conjunto de estos números se le denota por
 . Es decir
. Es decir 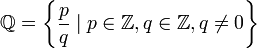
Definición de suma y multiplicación en Q
- Se define a la suma

- Se define a la multiplicación

Relaciones de equivalencia y orden en Q
- Se define la equivalencia
 cuando ad = bc
cuando ad = bc - Los racionales positivos son todos los
 tales que ab > 0
tales que ab > 0 - Los racionales negativos son todos los
 tales que ab <>
tales que ab <> - Se define el orden
 \frac{c}{d}"> cuando ad − bc > 0
\frac{c}{d}"> cuando ad − bc > 0
Notación
- Los números de tipo
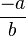 son denotados por
son denotados por 
- Las sumas de tipo
 son denotadas por
son denotadas por 
 denota a
denota a 
- Todo número
 se denota simplemente por p.
se denota simplemente por p.
Propiedades de los números racionales
El conjunto de los números racionales con la suma y multiplicación definida de esta manera forman un campo.
Propiedades de la suma y multiplicación
- La suma en Q es conmutativa, esto es:

- La suma en Q es asociativa, esto es:
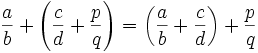
- La multiplicación en Q es conmutativa, esto es:
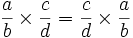
- La multiplicación en Q es asociativa, esto es:

- La multiplicación se distribuye en la suma, esto es

Existencia de neutros e inversos
- Para cualquier racional
 se cumple que
se cumple que 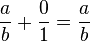 entonces
entonces  es el neutro aditivo de los racionales y se le denota por 0.
es el neutro aditivo de los racionales y se le denota por 0. - Para cualquier racional
 se cumple que
se cumple que 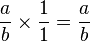 entonces
entonces  es el neutro multiplicativo de los racionales y se le denota por 1.
es el neutro multiplicativo de los racionales y se le denota por 1. - Cada número racional
 tiene un inverso aditivo
tiene un inverso aditivo 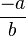 tal que
tal que 
- Cada número racional
 con excepción de 0 tiene un inverso multiplicativo
con excepción de 0 tiene un inverso multiplicativo  tal que
tal que 
Equivalencias notables en Q
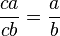 si y sólo si
si y sólo si 
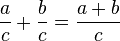



Los números enteros en Q
- Si p es un número entero entonces existe el número
 que equivale a p y mantiene todas sus propiedades de entero. Es decir, se define
que equivale a p y mantiene todas sus propiedades de entero. Es decir, se define 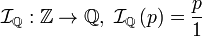
Otras notaciones de números en Q
Fracciones mixtas
Cada número racional  se puede expresar de forma única como
se puede expresar de forma única como  donde
donde
- A es un entero no negativo, es decir
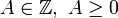
 es un racional irreducible no negativo menor que uno. Se expresa como
es un racional irreducible no negativo menor que uno. Se expresa como 
- u es una unidad. Es decir

La notación es muy sencilla, las reglas son
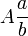 denota a
denota a 
 denota a
denota a 
Por ejemplo 
El conjunto de los números decimales en Q
- Un número decimal es un número racional de la forma

 denota al conjunto de los números de este tipo. Es decir
denota al conjunto de los números de este tipo. Es decir 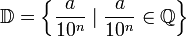
- Expresión decimal de un número decimal: el número a en base 10 con un punto a n lugares del extremo derecho, por ejemplo
 se denota como 1.78
se denota como 1.78
Representación decimal de los racionales
Los racionales se caracterizan por tener un desarrollo decimal cuya expresión sólo puede ser de tres tipos:
- Exacta: la parte decimal tiene un número finito de cifras. Ejemplo:
- Periódica pura: toda la parte decimal se repite indefinidamente. Ejemplo:
- Periódica mixta: no toda la parte decimal se repite. Ejemplo:
En efecto, al aplicar el algoritmo para dividir un entero por otro, sólo existen un número finito de restos posibles. Siendo la sucesión de restos infinita, aparecerá forzosamente un mismo resto en dos posiciones distintas. A partir de ellas, el cálculo se repite igual. Ejemplo:
Recíprocamente, todo número con un desarrollo decimal puede expresarse en fracción de la siguiente manera:
- Decimales exactos o finitos: Se escribe en el numerador la expresión decimal sin la coma, y en el denominador un uno seguido de tantos ceros como cifras decimales. Ejemplo:

- Decimales periódicos puros: La fracción de un número decimal periódico tiene como numerador la diferencia entre el número escrito sin la coma y la parte anterior al periodo; y como denominador, tantos "9" como cifras tiene el periodo. Ejemplo:

- Decimales periódicos mixtos: Tendrá como numerador la diferencia entre a y b, donde a es el número escrito sin la coma, y b es el número sin la parte decimal periódica, escrito como número entero. El denominador tendrá tantos "9" como cifras tiene el periodo y otros tantos "0" como cifras decimales no periódicas haya. Ejemplo: Sea el número
 entonces a = 1234567 y b = 12345, por lo que el número buscado será
entonces a = 1234567 y b = 12345, por lo que el número buscado será  .
.
Número real
Los números reales se definen de manera axiomática como el conjunto de números que se encuentran en correspondencia biunívoca con los puntos de una recta infinita (continuum): la recta numérica. El conjunto de los números reales se le simboliza con la letra  . El nombre de número real se propuso como antónimo de número imaginario.
. El nombre de número real se propuso como antónimo de número imaginario.
El concepto de número real se originó cuando se constató la existencia de los números irracionales. Así, el conjunto de los números reales se origina como la unión del conjunto de los números racionales y el conjunto de los irracionales.
Debido a que el conjunto de números reales contiene al conjunto de números racionales, y éste a su vez contiene a los enteros que a su vez contiene los números naturales, se sigue que el conjunto de los números reales contiene también a los números enteros y a los números naturales. Asimismo, el conjunto de números reales contiene al de los números irracionales.
Por tanto, los números reales pueden ser racionales o irracionales, algebraicos o trascendentes; y positivos, negativos, o cero.
Puede definirse un número real, en estos términos, como un número positivo o negativo que puede o no tener cifras de decimal finito o infinito y puede representarse mediante un punto en la recta de números reales. En este sentido, el teorema fundamental de la geometría analítica establece que a cada número real le corresponde un punto en la recta de los números reales y recíprocamente.
Con números reales pueden realizarse todo tipo de operaciones básicas con dos excepciones importantes:
1.- No existen raíces de orden par (cuadradas, cuartas, sextas, etc) de números negativos en números reales, razón por la que existe otro conjunto de números donde estas operaciones están definidas: los imaginarios.
2.- No existe la división entre cero, pues carece de sentido dividir entre nada o entre nadie, es decir, no existe la operación de dividir entre nada.
Estas dos restricciones tienen repercusiones importantes en ramas más avanzadas de las matemáticas: existen asíntotas verticales en los lugares donde una función se indefine, es decir, en aquellos valores de la variable en los que se presenta una división entre cero, o no existe gráfica real en aquellos valores de la variable en que resulten números negativos para raíces de orden par, por mencionar un ejemplo de construcción de gráficas en geometría analítica.
La principal característica del conjunto de los números reales es la completitud, es decir, la existencia de límite para dada sucesión de Cauchy de números reales.
Construcción axiomática
El conjunto de números reales, denotado por  es aquel que cada elemento cumple cada una de las siguientes proposiciones:
es aquel que cada elemento cumple cada una de las siguientes proposiciones:
- Si
 , entonces
, entonces  (Cerradura en la suma)
(Cerradura en la suma) - Si
 , entonces
, entonces  (Conmutatividad en la suma)
(Conmutatividad en la suma) - Si
 , entonces
, entonces  (Asociatividad en la suma)
(Asociatividad en la suma) - Existe
 de manera que
de manera que 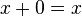 para cualquier
para cualquier 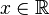 (Neutro aditivo)
(Neutro aditivo) - Para cada
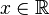 existe un elemento
existe un elemento  tal que
tal que  (Inverso aditivo)
(Inverso aditivo) - Si
 , entonces
, entonces  (Cerradura en la multiplicación)
(Cerradura en la multiplicación) - Si
 , entonces
, entonces  (Conmutatividad en la multiplicación)
(Conmutatividad en la multiplicación) - Si
 , entonces
, entonces 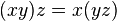 (Asociatividad en la multiplicación)
(Asociatividad en la multiplicación) - Existe
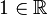 de manera que
de manera que  para cualquier
para cualquier 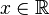 (Neutro multiplicativo)
(Neutro multiplicativo) - Para cada
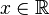 existe un elemento
existe un elemento  tal que
tal que  (Inverso multiplicativo)
(Inverso multiplicativo) - Si
 , entonces
, entonces  (Distributividad de la multiplicación en la suma)
(Distributividad de la multiplicación en la suma) - Si
 , entonces se cumple sólo una de estas: (Tricotomía)
, entonces se cumple sólo una de estas: (Tricotomía) - Si
 ,
,  y
y  entonces
entonces 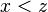 (Transitividad)
(Transitividad) - Si
 y
y  , entonces
, entonces  (Monotonía en la suma)
(Monotonía en la suma) - Si
 ,
,  y 0 < z, entonces
y 0 < z, entonces  (Monotonía en la multiplicación)
(Monotonía en la multiplicación)
Construcción por números decimales
Consideramos los números decimales como los conocemos intuitivamente. Sabemos que 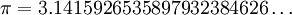 , es decir, el número π se expresa como el número entero 3 y una secuencia infinita de dígitos 1, 4, 1, 5, 9, 2, etc.
, es decir, el número π se expresa como el número entero 3 y una secuencia infinita de dígitos 1, 4, 1, 5, 9, 2, etc.
Un número decimal se expresa entonces como  donde x es un número entero y cada di es un elemento del conjunto {0,1,2,3,4,5,6,7,8,9}. Además, consideramos que no existen las colas de 9.
donde x es un número entero y cada di es un elemento del conjunto {0,1,2,3,4,5,6,7,8,9}. Además, consideramos que no existen las colas de 9.
Al conjunto de todos los números decimales donde x es un número entero positivo se le denota por 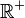 y se le llama el conjunto de los números reales positivos.
y se le llama el conjunto de los números reales positivos.
Al conjunto de todos los números decimales donde x es un número entero negativo se le denota por  y se le llama el conjunto de los números reales negativos.
y se le llama el conjunto de los números reales negativos.
Al número decimal  se le llama cero.
se le llama cero.
Al conjunto  se le denota por
se le denota por  y se le llama conjunto de números reales.
y se le llama conjunto de números reales.
Se define la relación de orden total de los números decimales como
 x\,"> para todo
x\,"> para todo 
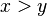 y\,"> siempre que
y\,"> siempre que  y
y 
 0\,"> para todo
0\,"> para todo 
- Dados dos números reales cualesquiera
 y
y  ,
, 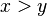 y\,"> en cualquiera de los casos siguientes:
y\,"> en cualquiera de los casos siguientes:  b\,">
b\,"> y además existe
y además existe  tal que
tal que  para todo
para todo  y
y  b_n\,">
b_n\,">
Número irracional
Tras distinguir los números componentes de la recta real en tres categorías: (naturales, enteros y racionales), podría parecer que ha terminado la clasificación de los números, pero aun quedan "huecos" por rellenar en la recta de los números reales.
Los números irracionales son los elementos de dicha recta que cubren los vacíos que dejan los números racionales.
Los números irracionales son los elementos de la recta real que no pueden expresarse mediante el cociente de dos enteros y se caracterizan por poseer infinitas cifras decimales que no siguen un periodo definido. De este modo, puede definirse número irracional como decimal infinito no periódico.
Toda expresión en números decimales es solo una aproximación en números racionales al número irracional referido, por ejemplo, el número racional 1.4142135 es solo una aproximación a 7 cifras decimales del número irracional raíz cuadrada de 2, el cual posee infinitas cifras decimales que no siguen un periodo.
Entonces, decimos con toda propiedad que el número raíz cuadrada de dos es aproximadamente igual a 1.4142135 en 7 decimales, o bien es igual a 1.4142135 ... , es decir, los tres puntos hacen referencia a los infinitos decimales que hacen falta y que jamás terminaríamos de escribir.
Debido a ello, los más célebres números irracionales son identificados mediante símbolos especiales; los tres principales son los siguientes:
- π (pi): relación entre el perímetro de una circunferencia y su diámetro.
- e:
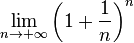
- Φ (número áureo):
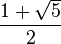
Los números irracionales se clasifican en dos tipos:
1.- Irracionales algebraicos: Son la solución de alguna ecuación algebraica y se representan por un número finito de radicales libres o anidados; si x representa ese número, al eliminar radicales del segundo miembro mediante operaciones inversas, queda una ecuación algebraica de cierto grado. Todas las raíces no exactas de cualquier orden son irracionales algebraicos.
Por ejemplo, el número áureo es una de las raíces de la ecuación algebraica:
x2 − x − 1 = 0, por lo que es un número irracional algebraico.
2.- Irracionales trascendentes: No pueden representarse mediante un número finito de raíces libres o anidadas; provienen de las llamadas funciones trascendentes: trigonométricas, logarítmicas y exponenciales. También surgen al escribir números decimales no periódicos al azar o con un patrón que no lleva periodo definido, respectivamente, como los dos siguientes:
0.193650278443757 ...
0.101001000100001 ...
Los llamados números trascendentes tienen especial relevancia ya que no pueden ser solución de ninguna ecuación algebraica.
El pi y e son irracionales trascendentes, puesto que no pueden expresarse mediante radicales.
Los números irracionales no son numerables, es decir, no pueden ponerse en biyección con el conjunto de los números naturales. Por extensión, los números reales tampoco son contables ya que incluyen el conjunto de los irracionales.
Número complejo
Los números complejos son una extensión de los números reales, cumpliéndose que  . Los números complejos representan todas las raíces de los polinomios, a diferencia de los reales.
. Los números complejos representan todas las raíces de los polinomios, a diferencia de los reales.
Los números complejos son la herramienta de trabajo del álgebra ordinaria, llamada álgebra de los números complejos, así como de ramas de las matemáticas puras y aplicadas como variable compleja, aerodinámica y electromagnetismo entre otras de gran importancia.
Contienen a los números reales y los imaginarios puros y constituyen una de las construcciones teóricas más dignas de la inteligencia humana. Los análogos del cálculo diferencial e integral con números complejos reciben el nombre de variable compleja o análisis complejo.
Definición
Definiremos cada complejo z como un par ordenado de números reales (a, b) ó (Re(z), Im(z)), en el que se definen las siguientes operaciones:
- Suma
- Multiplicación
- Igualdad
A la primera componente (a) se le llama parte real y a la segunda (b), parte imaginaria. Si un número tiene sólo parte imaginaria se dice que es imaginario puro.
Tal como los hemos definido, los números complejos forman un cuerpo, el cuerpo complejo, denotado por C (o más apropiadamente por el carácter unicode ℂ ). Si identificamos el número real a con el complejo (a, 0), el cuerpo de los números reales R aparece como un subcuerpo de C. Más aún, C forma un espacio vectorial de dimensión 2 sobre los reales. Los complejos no pueden ser ordenados como, por ejemplo, los números reales: C no puede ser convertido de ninguna manera en un cuerpo ordenado.
Unidad imaginaria
Tomando en cuenta que  , se define un número especial en matemáticas de gran importancia, el número i o unidad imaginaria, definido como
, se define un número especial en matemáticas de gran importancia, el número i o unidad imaginaria, definido como
- i = (0,1)
Luego,
Representación binomial
Cada complejo se representa en forma binomial como:
z = a + ib
a es la parte real del número complejo z, y b es su parte imaginaria. Esto se expresa así:
a = Re(z)
b = Im(z)
Plano de los números complejos o Diagrama de Argand
Desde un punto de vista geométrico la recta real (recta que representa el total de números reales) puede ser vista como un subconjunto del plano de los números complejos.
Cada número complejo sería un punto en ese plano. En la parte horizontal o eje real, se colocan los números reales; en el eje vertical o eje imaginario, van los números imaginarios puros.
Dado que cada número complejo consta de una parte real y una imaginaria, puede representarse geométricamente cada número complejo por sus coordenadas en el plano complejo, similarmente al plano de coordenadas cartesianas.
Valor absoluto o módulo, conjugado y distancia [editar]
Valor absoluto o módulo de un número complejo [editar]
El valor absoluto, módulo o magnitud de un número complejo z viene dado por la siguiente expresión:

Si pensamos en z como algun punto en el plano; podemos ver, por el teorema de Pitágoras, que el valor absoluto de un número complejo coincide con la distancia euclídea desde el origen del plano.
Si el complejo está escrito en forma exponencial z = r eiφ, entonces |z| = r. Se puede expresar en forma polar como z = r(cosφ + isenφ), donde cosφ + isenφ = eiφ es la conocida fórmula de Euler.
Podemos comprobar con facilidad estas cuatro importantes propiedades del valor absoluto




para cualquier complejo z y w.
Por definición, la función distancia queda como sigue d(z, w) = |z - w| y nos provee de un espacio métrico con los complejos gracias al que se puede hablar de límites y continuidad. La suma, la resta, la multiplicación y la división de complejos son operaciones continuas. Si no se dice lo contrario, se asume que ésta es la métrica usada en los números complejos.
Conjugado de un número complejo [editar]
Dos binomios se llaman conjugados si solo difieren en su signo central, por ejemplo, los dos binomios: 3m - 1 y 3m + 1 son conjugados.
El conjugado de un complejo z (denotado como  ó
ó 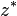 ) es un nuevo número complejo, definido así:
) es un nuevo número complejo, definido así:

Se observa que ambos difieren en el signo de la parte imaginaria.
Con este número se cumplen las propiedades:





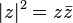
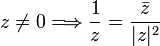
Esta última fórmula es el método elegido para calcular el inverso de un número complejo si viene dado en coordenadas rectangulares.
Representación trigonométrica (polar) y representación geométrica [editar]
Algunas veces, la representación de números complejos en la forma z = a + i b ("coordenadas rectangulares") es menos conveniente que otra representación, usando coordenadas polares.
Representamos el número complejo z en el plano de números complejos como un punto con coordenadas (a, b), denominado vector de posición.
Trazamos la distancia desde el punto (0,0) hasta (a, b), a la que llamaremos r, y, que como se ha visto antes, es igual al módulo de z, expresado | z | .
Esta distancia forma, con respecto al eje real positivo, un ángulo, denominado φ.
La representación polar nos permite expresar este número complejo en función de r y del ángulo φ:
z = rei(φ + 2πk)
Módulo y argumento [editar]
En esta representación,  es el módulo del número complejo y el ángulo
es el módulo del número complejo y el ángulo 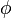 es el argumento del número complejo.
es el argumento del número complejo.

Formamos un triángulo rectángulo, con r como hipotenusa, y con catetos a y b. Vemos que:

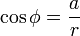
Despejamos a y b en las expresiones anteriores y, utilizando la representación binomial:

Sacamos factor común r:

(Frecuentemente, esta expresión se abrevia de la siguiente manera: z = rcisφ)
Según esta expresión, puede observarse que para definir un número complejo tanto de esta forma como con la representación binomial se requieren dos parámetros, que pueden ser parte real e imaginaria o bien módulo y argumento, respectivamente.
Según la Fórmula de Euler, vemos que:

No obstante, el ángulo φ no está unívocamente determinado por z, como implica la fórmula de Euler:
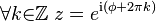
Por esto, generalmente restringimos φ al intervalo [-π, π] y a éste φ restringido lo llamamos argumento principal de z y escribimos φ = arg(z). Con este convenio, las coordenadas estarían unívocamente determinadas por z.
La multiplicación de números complejos es especialmente sencilla con la notación polar:

División:
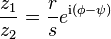
Potenciación:

| Sistema numérico en matemática. |
| Conjuntos de Números |
|
|
| Números destacables |
| Números Especiales |
|
| Números con propiedades especiales |
| Primos |
Identidad de Euler
Se llama identidad de Euler a una fórmula desarrollada por Leonhard Euler, notable por relacionar los cinco números más famosos de la historia de las matemáticas y que pertenecen a distintas ramas:
donde:
- π es el número más importante de la geometría
- e es el número más importante del análisis matemático
- i es el número más importante del álgebra
- 0 y 1 son las bases de la aritmética por ser los elementos neutros respectivamente de la adición y la multiplicación
Otra curiosidad de esta fórmula es que, si le escribimos de esta manera: 
representa la evolución del concepto de número a lo largo de la historia. Desde el concepto más intuitivo, los números naturales, conocidos desde la prehistoria, añadiendo los números negativos (representados por -1) obtenemos los números enteros. Luego, añadiendo las fracciones (no aparecen) obtenemos los racionales. Después, añadiendo los irracionales (e y π) obtenemos los números reales. Y finalmente, añadiendo los números imaginarios (representados por i) obtenemos los números complejos.
Volviendo a la primera fórmula, se puede ver que también cuenta la historia de una evolución en las matemáticas, en este caso de las operaciones aritméticas. Aparecen una suma, un producto y una potencia.
... / ecuaciones










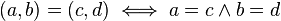


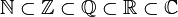


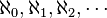 }
} ,
, 
No hay comentarios:
Publicar un comentario