Condiciones de continuidad de una función
Una función continua es aquella cuya regla de correspondencia asigna incrementos pequeños en la variable dependiente a pequeños incrementos de los elementos del dominio de dicha función, es decir,  , y usando la expresión Δy + y = f(Δx + x), queda
, y usando la expresión Δy + y = f(Δx + x), queda  donde en este caso, f(x) = y. Ello quiere decir que
donde en este caso, f(x) = y. Ello quiere decir que 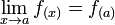 , y si este último límite existe significa en consecuencia por un Teorema de Límites (un límite existe sí y sólo si los dos límites laterales existen y son iguales) que toda función f(x) que cumpla con
, y si este último límite existe significa en consecuencia por un Teorema de Límites (un límite existe sí y sólo si los dos límites laterales existen y son iguales) que toda función f(x) que cumpla con
 es continua en el punto a.
es continua en el punto a.
Condición no recíproca
La relación no funciona a la inversa: el que una función sea continua no garantiza su derivabilidad. Es posible que los límites laterales sean equivalentes pero las derivadas laterales no, en este caso la función presenta un punto anguloso en dicho punto.
Un ejemplo puede ser la función módulo en el punto (0, 0). Dicha función es equivalente a la función partida 
Para valores infinitamente cercanos a 0, por ambas ramas, el resultado tiende a 0. Y el resultado en el punto 0 es también 0, por lo tanto es continua. Sin embargo, las derivadas resultan 
Cuando x vale 0, las derivadas laterales dan resultados diferentes. Por lo tanto, no existe derivada en el punto, a pesar de que sea continuo.
Funciones reales de una variable real
Introducción
Informalmente hablando, una función f definida sobre un intervalo I es continua si la curva que la representa, es decir el conjunto de los puntos (x, f(x)), con x en I, está constituida por un trazo continuo, es decir que se puede dibujarla sin levantar el lápiz del papel, como en la figura de la izquierda.
El intervalo I de x es el dominio de definición de f, definido como el conjunto de los valores de x para los cuales f(x) existe.
El intervalo J de y es el codominio (también conocido como contradominio, rango o imagen) de f, el conjunto de los valores de y, tomados como y = f(x). Se escribe J = f(I).
El mayor elemento de J' se llama el máximo absoluto de f en I, y el menor valor de J es su mínimo absoluto en el dominio I.
Continuidad de una función en un punto
En el caso de aplicaciones de  en
en  , y de una manera más rigurosa se dice que una función; f es continua en un punto x1 si existe f(x1), si existe el límite de f(x) cuando x tiende hacia x1 por la derecha, si existe el límite de f(x) cuando x tiende hacia x1 por la izquierda, y además coinciden con f(x1).
, y de una manera más rigurosa se dice que una función; f es continua en un punto x1 si existe f(x1), si existe el límite de f(x) cuando x tiende hacia x1 por la derecha, si existe el límite de f(x) cuando x tiende hacia x1 por la izquierda, y además coinciden con f(x1).
Así pues, una función f continua en el punto x1 implica lo siguiente:
- Existe f(x1):
- tiene limite por la izquierda:
- tiene limite por la derecha:
- El límite por la derecha por la izquierda y el valor de la función coinciden:
Es decir: el límite de la tasa de variación es cero cuando el incremento de la variable independiente , h, tiende a cero:
Una definición más exacta es
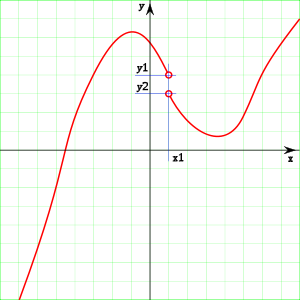
Si f(x1)= y1, la continuidad en x1 se expresa así:
parafraseando, cuando x se aproxima a x1, f(x) se aproxima a y1. Por definición de los límites, esto significa que para todo intervalo abierto J, centrado en y1, existe un intervalo abierto I, centrado en x1, tal que  .
.
Si f ejecuta un salto en el punto, el teorema cae en falta. En efecto no todo intervalo I alrededor de x1 tiene su imagen en un intervalo J centrado en y1, con un radio inferior al salto de f, no importa lo pequeño que este intervalo sea, hay valores de x del intervalo I alrededor de x1 que tiene su imagen en un intervalo K centrado en y2, siendo y1 y y2 valores distintos, esto es: x tiene imágenes que se salen de J.
La ventaja de esta definición es que se generaliza a cualquier espacio topológico.
Continuidad lateral
Una función f es continua por la izquierda en el punto x = x1 si el límite lateral por la izquierda y el valor de la función en el punto son iguales. Es decir:
como en la figura.
Una función f es continua por la derecha en el punto x = x1 si su límite lateral por la derecha y el valor de la función en el punto son iguales. Es decir :
Una función f es continua en un punto si es continua por la izquierda y es continua por la derecha. Esto es:
Continuidad de una función en un intervalo
Una función, f es continua en un intervalo I, si y sólo si la función es continua en todos los puntos del intervalo, es decir:
- f es continua en un intervalo I ⇔

Dado que una función f es continua en un intervalo abierto (a, b) si la función es continua en todos los puntos del intervalo, entonces f es continua en el intervalo cerrado [a, b] si y sólo si es continua en el intervalo (a, b) y además es continua en el punto a por la derecha y en el punto b por la izquierda.
La función anterior es continua tanto en [-6, 1) como en (1, 6].
Algunas funciones continuas importantes
Las funciones polinomiales, trigonométricas: seno y coseno, las exponenciales y los logaritmos son continuas en sus respectivos dominios de definición.
La parábola, como función polinómica, es un ejemplo de función continua a lo largo de todo el dominio real.
En la gráfica se ve la función seno que es periódica, acotada y continua en todo el domino real, dado su carácter periódico, con ver uno solo de los ciclos es suficiente para comprobar la continuidad, porque el resto de los ciclos son exactamente iguales.
Algunas funciones discontinuas
Los * En los y las funciones racionales: son discontinuas en los puntos donde el denominador se hace cero. Un ejemplo de esto es la función inverso:
El denominador se hace cero para x = 1.
Esta función es una hipérbola compuesta por dos tramos. x x > 1. Como vemos, efectivamente es continua en todo su dominio  pero no esta definida en x= 1 por lo que no es una función continua. Aunque este formada por dos ramas continuas cada una de por si.
pero no esta definida en x= 1 por lo que no es una función continua. Aunque este formada por dos ramas continuas cada una de por si.
- La función raíz: para los valores de x, en los que el radicando toma valores negativos:
La función seno toma valores positivos y negativos, la raíz de números negativos no esta definida para  , donde la función es discontinua.
, donde la función es discontinua.
- La función trigonométrica Tangente es periódica y discontinua para π / 2 en cada ciclo.
Funciones definidas por intervalos
La funciones definidas para distintos intervalos de x, puede ser discontinua en los puntos de cambio de intervalo, como por ejemplo:
- La Función parte entera de x, E(x), donde E(x) es el mayor número entero inferior o igual a x, tal que:
- E(x) ≤ x x) + 1.
Su curva es una sucesión de segmentos horizontales a distintas alturas. Esta función no es continua en los enteros, pues los límites a la izquierda y a la derecha difieren de uno, pero es continua en los segmentos abiertos (n, n+1) donde es constante.
- Otras funciones definidas por intervalos
Funciones que no son continuas en ninguna parte
Existen funciones que no son continuas en ningún punto. La más conocida es la función característica de Q, es decir la función que toma como valor 1 cuando x pertenece al conjunto de los racionales, y 0 si no.
Obviamente, no se puede dibujar su curva, que está constituida por una infinidad de puntos en la recta y= 0 , y una infinidad (menor) de puntos en la recta y= 1.
Tipos de discontinuidades
Ahora vemos distintos casos de funciones que son continuas en todos los puntos de un intervalo excepto en un número finito de puntos. Con esto queremos decir que, si tomamos un punto en concreto del intervalo en el que la función no es continua, podemos encontrar otro nuevo intervalo más pequeño en el que el punto tomado sea el único punto en el que la función no es continua.
Discontinuidad evitable
Una función presenta un punto de Discontinuidad evitable (o removible) si en ese punto se cumple que:
Pueden ser transformadas en otra función continua, dándole a f(x1) el valor adecuado que la hace continua. Si modificamos una función obtenemos otra función, no la misma, por ello se dice que son evitables.
- ejemplo:
La función:
Presenta los siguientes limites por la izquierda y por la derecha:
pero la función para x= 2 no esta definida:
en este un caso de discontinuidad evitable y además de un modo sencillo:
lo que es lo mismo:
simplificando:
esta función es continua para todo x de valor real y es equivalente a la primera función, excepto en que la primera es discontinua para x= 2.
Discontinuidad de primera especie
Una función presenta una discontinuidad de primera especie en un punto x1, si en este punto se cumple que:
se produce un salto en los extremos.
Discontinuidad de segunda especie
Son las que tienen puntos para los que existe solo uno o ningún límite. Por ejemplo la función  . Ésta tiene una discontinuidad de segunda especie en 0 pues no existe el límite
. Ésta tiene una discontinuidad de segunda especie en 0 pues no existe el límite 
 o
o 
Discontinuidad asintótica
La discontinuidad viene marcada por una asíntota vertical. Se cumple lo siguiente:
Más información en: función discontinua
Derivabilidad implica continuidad
Si una función es derivable en x= a entonces es continua en x= a.
Hipótesis: Existe f'(a)
Tesis: f(x) es continua en x= a
Demostración:
Es importante notar que el recíproco no es válido; es decir que nada se puede afirmar sobre la derivabilidad de una función continua. Un ejemplo claro de esta situación es la función valor absoluto f(x)= |x| que si bien es continua en todo su dominio no es derivable en x= 0
Teoremas sobre funciones continuas
Estos son algunos de los teoremas más importantes sobre funciones continuas.
- Teorema de Weierstrass: Si f es continua en [a,b] entonces presenta máximos y mínimos absolutos.
- Teorema de Bolzano: Si f es continua en [a,b] y f(a) > 0 y f(b) <>, entonces
![\exists c \in ]a,b[](http://upload.wikimedia.org/math/9/f/5/9f565f8f3dfaa671a4b1b3246e2c47d8.png) tal que f(c) = 0
tal que f(c) = 0 - Teorema del valor intermedio: Si f es continua en [a,b] y f(a) < k < f(b) entonces
![\exists c \in ]a,b[](http://upload.wikimedia.org/math/9/f/5/9f565f8f3dfaa671a4b1b3246e2c47d8.png) tal que f(c) = k
tal que f(c) = k






![\lim_{h \to 0} [f(x1+h) - f(x1)] = 0](http://upload.wikimedia.org/math/e/a/6/ea628bf43ee2f21915af3b6b49ee5b44.png)















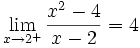





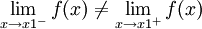









No hay comentarios:
Publicar un comentario