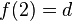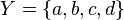Funciones: Pares ordenados y plano cartesiano, nociones funciones, dominio y rango de una función, gráfica de una función.

Función

La palabra Función puede hacer referencia a:

una función informática: subprograma o subrutina que realiza una tarea específica y devuelve un valor;
una función semiótica: conjunto de elementos y las relaciones entre ellos que son necesarios para definir una estructura;
una función técnica: el pasaje, mediante un dispositivo apropiado, de un conjunto dado de estados iniciales de un sistema, a un estado final deseado.
una función teatral, representación artística de una obra.
una función matemática: correspondencia o relación f de los elementos de un conjunto A con los elementos de un conjunto B

Si a cada elemento x de un conjunto X se le hace corresponder, mediante una regla o fórmula, un elemento y, y sólo uno de otro conjunto Y, dicha correspondencia se denomina función. El conjunto X se llama Dominio de la función y el conjunto Y Contradominio (codominio) o Dominio de imágenes.

Una función es pués un conjunto de pares ordenados (x, y) en donde no puede haber dos parejas distintas en que se repita el primer elemento.

Definición de función de una variable:

Sea X un conjunto de números reales, una función f de una variable es una correspondencia que asocia a cada número x que pertenece a X uno y sólo un número real y que pertenece a un conjunto Y. Cada elemento de Y queda notado y determinado por y = f (x).

Correspondencia matemática

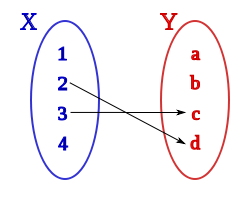
Dados dos conjuntos: X e Y, y un grafo f, que determina alguna Relación matemática entre elementos de X con algunos elementos de Y, diremos que ese grafo: f, define una correspondencia entre X e Y, que representaremos:

$f: X \rightarrow Y$

cuando al menos un elemento de X está relacionado con al menos un elemento de Y.

Definiciones

En una correspondencia podemos distinguir distintos conjuntos:

Conjunto inicial: es el primero de la correspondencia, es este caso X, lo representaremos: in (f), según el ejemplo:

$X = in (f) = \{1, 2, 3, 4 \} \,$

Conjunto final: es el segundo de la correspondencia en este caso Y, lo representaremos como fin (f), según el ejemplo:

$Y = fin (f)= \{a, b, c, d \} \,$

Conjunto origen: es el formado por los elementos del conjunto inicial, que están relacionados con algún elemento del conjunto final, lo representaremos or (f), en el ejemplo será:

$or (f)= \{2, 3 \} \,$

Conjunto imagen: es el formado por los elementos del conjunto final con los que están relacionados los elementos del conjunto origen, lo representaremos im (f), en el ejemplo:

$im (f) = \{ c, d \} \,$

Elementos homólogos: dos elementos, uno del conjunto origen y otro del conjunto imagen, se dice que son homólogos, si están relacionados según la correspondencia f, en el ejemplo los siguientes pares ordenadas son homólogos:

$(2, d), \; (3, c)$

Imagen de un elemento: dado un elemento x del conjunto origen, y otro elemento y del conjunto imagen, se dice que y es imagen de x y se representa:

$f(x) = y \,$

si el elemento x esta relacionado con el elemento y según la correspondencia f. en el ejemplo tenemos que:

$f(2) = d \,$

$f(3) = c \,$

Correspondencia definida a partir del producto cartesiano

Dados los conjuntos X (Conjunto inicial) e Y (Conjunto final) y definido el producto cartesiano $X \times Y$ , de estos dos conjuntos, como el conjunto de pares ordenados (x, y), donde $x \in X$ e $y \in Y$ , dado el conjunto F que contiene a los pares homónimos de la correspondencia f, y $F \subset ( X \times Y )$ define esa correspondencia en su totalidad.

Por lo tanto podemos decir que una correspondencia entre dos conjuntos X e Y, es un subconjunto F del producto cartesiano $X \times Y$ , que recoge los pares ordenados (x, y), que forman la correspondencia.

ejemplo:

d	(1,d)	(2,d)	(3,d)	(4,d)
c	(1,c)	(2,c)	(3,c)	(4,c)
b	(1,b)	(2,b)	(3,b)	(4,b)
a	(1,a)	(2,a)	(3,a)	(4,a)
X×Y	1	2	3	4

en la diagrama anterior, tenemos los conjuntos:

$X = \{1, 2, 3, 4 \} \,$

$Y = \{a, b, c, d \} \,$

el producto $X \times Y$ se:

$X \times Y$	$= \{ \,$	$(1,a), \, (1,b), \, (1,c), \, (1,d),$
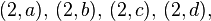		$(2,a), \, (2,b), \, (2,c), \, (2,d),$
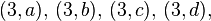		$(3,a), \, (3,b), \, (3,c), \, (3,d),$
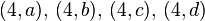		$(4,a), \, (4,b), \, (4,c), \, (4,d)$	$\} \,$

el conjunto F es el siguiente:

$F = \{ ( 2, d ), ( 3, c ) \} \,$

se puede apreciar que $F \subset ( X \times Y )$ y que F define la correspondencia en su totalidad.

Correspondencia inversa

Dada una correspondencia entre los conjuntos X e Y, representada:

$f: X \rightarrow Y$

se define como correspondencia inversa de f, que llamaremos $f^{-1} \,$ :

$f^{-1}: Y \rightarrow X$

a la que asocia la imagen de la función f con su origen.

Definida una correspondencia F, como un subconjunto del producto cartesiano de $X \times Y$ , donde los pares ordenados (x, y) son los asociados por la correspondencia, la correspondencia inversa $F^{-1} \,$ , es el subconjunto del producto cartesiano $Y \times X$ , formado por los pares ordenados (y, x) obtenidos de cambiar el orden de la correspondencia F.

Tipos de correspondencias

Correspondencia unívoca y biunívoca

Partiendo de dos conjuntos, uno inicial X, y otro final Y, y todas las posibles correspondencias que se pueden hacer entre estos dos conjuntos, por su interés podemos diferenciar las correspondencias unívocas y biunívocas.

Una correspondencia es unívoca si cada elemento inicial solo tienen una imagen.

Una correspondencia es biunívoca si cada elemento inicial solo tienen una imagen, y cada elemento imagen solo tiene un origen.

No es necesario en ninguno de los dos casos, que todos los elementos de X tengan una imagen, ni que todos los elementos de Y tengan un origen, claramente una correspondencia tiene que ser unívoca para poder ser biunívoca.

Si representamos con un rectángulo todas las posibles correspondencias entre los conjuntos X e Y, si el conjunto B es el de las correspondencias unívocas, y al A el de las biunívocas, en un Diagrama de Venn, se ve claramente que el conjunto de las correspondencias biunívocas es un subconjunto de las correspondencias unívocas.

Correspondencia no unívoca

Correspondencia no unívoca: es la que al menos uno de los elementos origen tiene dos o más imágenes. En el diagrama de Venn, son las correspondencias que no pertenecen a B: B’

Si el conjunto inicial es el de los alumnos de un centro escolar, y el conjunto final el de las asignaturas que se imparten en ese centro, la correspondencia de alumnos con asignaturas, no será unívoca cuando al menos un alumno estudia dos o más asignaturas.

En el diagrama de la figura el elemento 3 tiene dos imágenes b y c, esto hace que la correspondencia no sea unívoca, independientemente de la relación que tengan el resto de los elementos. Esta doble imagen para un único origen da lugar a que podamos decir:

$f(3) = b \,$

$f(3) = c \,$

Siendo las dos expresiones ciertas.

Correspondencia unívoca, no biunívoca

Correspondencia unívoca, no biunívoca: es la que a cada origen le corresponde una única imagen, pero no todas las imágenes tienen un único origen. En el diagrama de Venn, son las correspondencias que pertenecen a B pero no a A: B-A.

Si el conjunto inicial es el de las personas de una población, y el conjunto final el de los domicilios de esa población, la correspondencia de personas con domicilios, será unívoca pero no biunívoca cuando, cada persona viva en un único domicilio y en algún domicilio vivan varias personas.

La correspondencia representada en este diagrama es unívoca, pero no es biunívoca porque el elemento d, tiene dos orígenes: 1 y 2. Así tenemos que:

$f(1) = d \,$

$f(2) = d \,$

esto hace que no sea una correspondencia biunívoca, aunque por el resto de las relaciones si pueda serlo.

Correspondencia biunívoca

Correspondencia biunívoca: es la correspondencia en la que a los elementos origen tienen una única imagen, y los elementos imagen tienen un único origen. En el diagrama de Venn son las correspondencias que pertenecen a A.

Si tomamos como conjunto inicial el de personas, y por conjunto final el de automóviles, esta correspondencia será biunívoca, cuando las personas que tienen automóvil tienen un solo automóvil, y cada automóvil tenga un solo propietario.

En el diagrama de la figura se ve que:

$f(2) = a \,$

$f(3) = b \,$

$f(4) = d \,$

siendo estas todas las relaciones de esta correspondencia. Los elementos origen tienen una única imagen, y los elementos imagen tienen un único origen, puede haber elementos sin imagen como el 1, y elementos sin origen como la c, pero esto no influye en la consideración de correspondencia ni en sus tipos.

Función matemática

En Matemáticas, una función o aplicación del conjunto A en el conjunto B asocia a cada uno de los elementos de A uno y sólo un elemento de B.

Definición Matemática de una función

Desde un punto de vista formal, se dice que f es una función o aplicación de A en B y se denota

$f \colon A \to B \,$

y satisface:

$\forall a \in A \quad \rm {\exists b} \in B\mid (a,b) \in f$
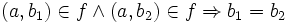
Si $(a,b_1) \in f \and (a,b_2) \in f \Rightarrow b_1 = b_2$

Esto significa que a cada elemento a de A, le corresponde por f un elemento b, y sólo uno, de B, al que se denomina imagen de a por f y que se denota $f(a)=b \,$ en vez de $(a,b)\in f$ .

En algunos textos de matemática se reserva la palabra función para el caso en que el conjunto B es un conjunto numérico y se utiliza aplicación para el caso más general de conjuntos cualesquiera. Esta distinción no está generalizada y se trata, en todo caso, de una distinción informal y de uso discrecional.

Dominio, conjunto de llegada y conjunto imagen

El dominio de una función es el conjunto de existencia de la misma, o sea los valores para los cuales la función está definida. Entonces, el dominio de una función f es el conjunto de todos los objetos que puede transformar. Se denota Dom f o Df.

$D_f = \left\{x \in A \mid \exists y \in B \mid (x,y) \in f\right\}$

Obsérvese que la condición de existencia de la definición de función garantiza que, si $f \colon A \to B \,$ es una función, entonces

D f = A

El codominio de una función $f \colon A \to B \,$ es el conjunto $B \,$ .

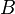Obsérvese que algunos elementos del codominio pueden no ser imagen de ningún elemento del dominio. Puede haber algún $y \in B$ tal que $\forall x \in A \;\, (x,y)\notin f$

El conjunto imagen, también llamado recorrido o rango, está formado por los valores que alcanza la función. Entonces, la imagen de una función f es el conjunto de todos los valores que toma la variable dependiente. Se denota Im f o If.

$Im_f = \left\{y \in B \mid \exists x \in A \mid (x,y) \in f\right\}$

Por ejemplo, la función f(x) = x + 1 tiene como dominio e imagen todos los números reales, pero una función g(x) = x², si bien tendrá como dominio a todos los reales, sólo tendrá como imagen los valores comprendidos entre 0 y +∞ que sean el cuadrado de un número real (de hecho, todos lo son).

Siempre es posible restringir tanto el conjunto dominio e imagen de una función con un propósito determinado. Por ejemplo, si se quiere restringir f(x) = x² para que sea biyectiva, es posible tomar una sola de las ramas de modo que el dominio restringido y el conjunto imagen tomen valores del intervalo [0,+∞).

Cantidad de variables

El dominio y la imagen pueden tener una única variable, o bien varias. De acuerdo a dichas cantidades se le pueden dar diferentes nombres a la función

$\mathbb{R}\rightarrow \mathbb{R}$ es una función escalar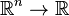
$\mathbb{R}^n \rightarrow \mathbb{R}$ es un campo escalar
$\mathbb{R} \rightarrow \mathbb{R}^n$ es una función vectorial
$\mathbb{R}^n \rightarrow \mathbb{R}^m$ es un campo vectorial

Se debe notar que la presencia de varias variables no afecta los criterios ya definidos sobre lo que es una función y lo que es sólo una Relación matemática. Dado un $(a, b)$ puede ocurrir que $a = b$ , pero el elemento que pertenece al dominio y que debe tener una y sólo una imagen es $(a, b)$ , no $a$ o $b$ en forma individual.

Conceptos para funciones de valor real

Para funciones 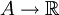$A\to\mathbb{R}$ tenemos:

Conjunto de ceros: Es el conjunto de puntos pertenecientes al dominio de la función para los cuales dicha función vale cero.

$C_0 = \left\{x \in D_f\mid f(x) = 0\right\}$

Conjunto de negatividad: Es el conjunto de puntos pertenecientes al dominio de la función para los cuales dicha función toma valores negativos.

Conjunto de positividad: Es el conjunto de puntos pertenecientes al dominio de la función para los cuales dicha función toma valores positivos.

$\text{[math]}$ 0\right\}">

Funciones inyectivas, sobreyectivas y biyectivas

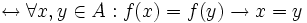Función inyectiva: Si cada elemento del conjunto es imagen de un único elemento del dominio. $f: A \rightarrow B\,$ es inyectiva $\harr \forall x,y \in A : f(x) = f(y) \rarr x = y$ ; o lo que es lo mismo: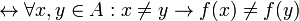 $\harr \forall x,y \in A : x \neq y \rarr f(x) \neq f(y)$
Función sobreyectiva: $f: A \rightarrow B\,$ es sobreyectiva si el conjunto imagen coincide con el conjunto B (conjunto de llegada o codominio). $f: A \rightarrow B\,$ es sobreyectiva $\harr \forall y \in B : \exists x \in A : f(x) = y$
Función biyectiva: 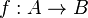$f: A \rightarrow B$ es biyectiva si $f \,$ es inyectiva y sobreyectiva.

Sobreyectiva, no inyectiva	Inyectiva, no sobreyectiva
Biyectiva	No sobreyectiva, no inyectiva

Álgebra de las funciones

Composición de funciones

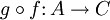Dadas dos funciones $f \colon A \to B \,\;$ y $g \colon B \to C \,\;$ tales que la imagen de $f \,$ está contenida en el dominio de $g\,$ , se define la función composición $\;\;g\circ f \colon A \to C \,$ como el conjunto de pares $(\,x, g(f(x)\,))$ , para todos los elementos $x \,$ de $A \,$ .

$A \to \,\,B\;\; \to \;\;\,C$

$x \mapsto f(x) \mapsto g(f(x))$

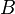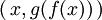Dado $x\,$ conocemos $(\, x, f(x) \,)$ , puesto que conocemos la función $f\,$ , y dado cualquier elemento $y \,$ de $B \,$ conocemos también $(\,y, g(y)\, )$ , puesto que conocemos la función $g \,$ . Por tanto, $(\, x, g(f(x)) \,)$ está definido para todo x. Luego $\;\;g\circ f \;$ cumple la condición de existencia que se exige a las funciones.

También cumple la condición de unicidad, dado que para cada $x \,$ el valor de $f(x) \,$ es único, y para cada $f(x) \,$ también lo es el de $g(f(x)) \,$ , por ser $f \;$ y $g \;$ funciones.

La composición de funciones es asociativa:

$h\circ (g \circ f) = (h\circ g) \circ f$

Sin embargo, en general, la composición de funciones no es conmutativa. Dadas $f \colon A \to B \,$ y $g \colon B \to C \,$ , $f\circ g\,$ puede no tener ni siquiera sentido, porque $g \,$ “devuelve” elementos de $C \,$ , en tanto que $f \,$ está definida en el dominio $A \,$ . Pero incluso en los casos en que dominios y codominios son compatibles (o son el mismo conjunto), nada garantiza que la composición de funciones sea conmutativa. Por ejemplo, con funciones numéricas $f(x)=x+1 \,\;$ y $\,g(x)=x^2 \,\;$ , $\,f(g(x))=x^2+1 \,\;$ , en tanto que $\;g(f(x))=(x+1)^2 \,$

Función identidad

Dado un conjunto $\, A \,$ , la función $\; e_A \colon A \to A \,$ que asigna a cada $x \,$ de $A \,$ el mismo $x \,$ de $A \,$ se denomina función identidad o función unitaria.

$e_A = \left\{(x, x)\mid x \in A \right\}$

Dada cualquier función $g \colon A \to B \,$ , es claro que $e_B\circ f \colon A \to B \,$ es igual a $f\,$ y que $f\circ e_A \colon A \to B \,$ es también igual a $f\,$ , puesto que para todo $x \;\; f(e_A(x))=f(x)$ y también $\;\; e_B(f(x))=f(x)$

$\; e_B \circ f = f \circ e_A = f \;$

Función inversa

Dada una función $f \colon A \to B \,\;$ , se denomina función inversa o función recíproca de $f \;$ , $f^{-1} \colon B \to A \,$ a la función que cumple la siguiente condición:

$\; f^{-1} \circ f = e_A \;$

$\; f \circ f^{-1} = e_B \;$

Si existe una función que cumpla esas dos condiciones, ser inversa por la izquierda y ser inversa por la derecha, se demuestra que esa función es única. Eso justifica la notación 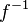$f^{-1} \;$ , que sería ambigua si pudiera haber dos inversas de la misma función.

Sólo algunas funciones tienen inversa. De hecho, la condición necesaria y suficiente para la existencia de 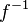$f^{-1} \;$ es que $f \;$ sea biyectiva. Por tanto, las afirmaciones

Existe función inversa de $f \;$ y
$f \;$ es biyectiva

son lógicamente equivalentes.

El grupo de las funciones biyectivas

Considerando todas las funciones biyectivas $f \colon \, A \to A$ , las conclusiones del apartado anterior pueden resumirse en:

Dadas tres funciones la operación de composición es asociativa: $(f_i \circ f_j) \circ f_k = f_i \circ (f_j \circ f_k) \,$
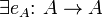$\exists e_A \colon \, A \to A \,$ tal que $\forall f\colon A \to A$ tenemos $f\circ e_A = e_A \circ f = f$
$\forall f \colon \, A \to A \, \exists f^{-1} \colon \, A \to A \mid f^{-1} \circ f = f\circ f^{-1} = e_A$

Estas tres condiciones determinan un grupo. El conjunto de las funciones biyectivas $A \to A$ es un grupo con respecto a la operación de composición de funciones y recibe el nombre de grupo simétrico de $A\,$ .

Funciones reales de variable real

Los anteriores apartados se han referido a funciones entre conjuntos cualesquiera. Las funciones entre conjuntos de números, y particularmente las funciones 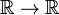$\mathbb {R} \to \mathbb {R}$ , o funciones reales de variable real son particularmente relevantes por la diversidad de sus aplicaciones prácticas y por sus particulares propiedades matemáticas. En algunos textos se reserva para las funciones entre conjuntos de números el término función mientras que a las funciones entre conjuntos cualesquiera se las denomina aplicaciones. A continuación se detallan algunas propiedades y definiciones de interés referidas a las funciones definidas 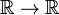$\mathbb {R} \to \mathbb {R}$ o entre conjuntos de números ( $\mathbb{N,Z,Q,R,C}$ ).

Funciones reales y funciones discretas

Si el dominio de una función es un intervalo de la recta real la función se denominará real. En cambio, si la función está definida para los números enteros se denominará función discreta. Un ejemplo de una función discreta son las sucesiones.

Funciones acotadas

Una función se denomina acotada si su conjunto imagen está acotado, por ejemplo: f(x) = sen(x) y g(x) = cos(x) tienen por conjunto imagen el intervalo [-1,1]. Si su conjunto imagen está acotado sólo superior o inferiormente, se dice que la función está acotada superior o inferiormente, respectivamente. Por ejemplo, f(x)=|x| tiene por conjunto imagen 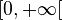$[0,+\infty[\;\!$ , por lo que está acotada inferiormente.

Funciones pares e impares

Se dice que una función es par cuando presenta simetría sobre el eje de ordenadas, esto es, si

$\forall x (x \in A \and -x \in A \rarr f(x) = f(-x))$

Una función es impar si presenta simetría con respecto al origen de coordenadas, esto es si

$\forall x (x \in A \and -x \in A \rarr f(x) = -f(-x))$

Una función que no presenta simetría par no tiene necesariamente simetría impar. Algunas funciones no presentan ninguno de los dos tipos de simetría o bien la presentan frente a focos o ejes distintos del origen de coordenadas o el eje de ordenadas (o eje Y)

... / funciones básicas

mat

jueves, 3 de mayo de 2007

Funciones