Función exponencial
En términos generales, una función es exponencial si se expresa de la forma
siendo a y k reales.
La expresión función exponencial se reserva para la inversa de la función logaritmo natural o, dicho en otros términos, para el caso en que a = e. Con esa definición, su dominio es R, pero se puede ampliar al cuerpo de los complejos.
Esta función se nota exp: R → R+*
donde e es la base de los logaritmos naturales.
-
-
- y = exp x <=> x = ln y (con y >0)
-
La tangente en x = 1, T1, pasa por el origen. La tangente en x = 0, T0, pasa por el punto (-1, 0).
Propiedades
Todas sus propiedades provienen de las propiedades del logaritmo. Se llama (función) exponencial la función definida sobre los reales por x →ex.
- La exponencial es la única función que es siempre igual a su derivada (de ahí su especial interés en el análisis, más precisamente para las ecuaciones diferenciales), y que toma el valor 1 cuando la variable vale 0.
- La exponencial transforma una suma en una constante
- su límite en - ∞ es 0, y en + ∞ es + ∞
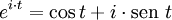 .
.
- Un caso particular de esta relación es la identidad de Euler, conocida también como la fórmula más importante del mundo. Más generalmente:
Se observa en los gráficos que si a > 1 la curva será creciente.
Derivada
La importancia de las funciones exponenciales en matemática y ciencias radica principalmente de las propiedades de su derivada. En particular,
Es decir, ex es su propia derivada. Es la única función con esa propiedad (sin tomar en cuenta la multiplicación de la función exponencial por una constante). Otras formas de expresar lo anterior:
- La pendiente del gráfico en cualquier punto es la altura de la función en ese punto.
- La razón de aumento de la función en x es igual al valor de la función en x.
- La función es solución de la ecuación diferencial y' = y.
Definición formal
La función exponencial ex puede ser definida de diversas maneras equivalentes entre sí, como una serie infinita. En particular puede ser definida como una serie de potencias:
o como el límite de la sucesión:
,,, / geometria


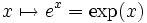

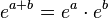




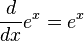
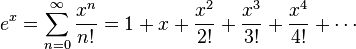

No hay comentarios:
Publicar un comentario