logaritmos

Logaritmo

En Matemática, el logaritmo es la función inversa de la función potencia x = bⁿ, que permite obtener n. Esta función se escribe como n = log_b x. Es el exponente o potencia a la que un número fijo, llamado base, se ha de elevar para dar un número dado. Por ejemplo, en la expresión 10² = 100, el logaritmo de 100 en base 10 es 2. Esto se escribe como log₁₀ 100 = 2.

Por ejemplo:

3⁴ = 81

El logaritmo es una de tres funciones relacionadas entre sí: en bⁿ = x, b puede ser encontrado con radicales, n con logaritmos y x con exponenciación. Se denomina logaritmo neperiano o logaritmo natural (ln) al logaritmo en base e de un número.

Logaritmos en otras bases

La elección de un determinado número como base de los logaritmos no es crucial, debido a que se pueden hacer conversiones de una base a otra de forma sencilla. Para ello, es útil la siguiente fórmula que define al logaritmo de x en base b (suponiendo que b, x, y k son números reales positivos y que tanto "b" como "k" son diferentes de 1):

en la que "k" es cualquier base válida. Si hacemos k=x, obtendremos:

En la práctica, se emplea el logaritmo decimal, que se indica como , en ciencias que hacen uso de las matemáticas, como la química en la medida de la acidez (denominada pH) y en física en magnitudes como la medida de la luminosidad (candela), del sonido(dB), de la energía de un terremoto (escala de Richter), etc. En informática se usa el logaritmo en base 2 la mayoría de veces. Las propiedades de los logaritmos son una base que facilita aún más su resolución.

Propiedad fundamental

La denominada propiedad fundamental, definida por:

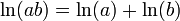(1) (con a>0 y b>0)

fue la que permitió construir las primeras tablas de logaritmos, cuyo propósito era hacer que calcular un producto fuese tan rápido como hallar una suma. En efecto, para calcular un producto se buscaban en la tabla los logaritmos de los factores, se sumaban, y se buscaba el número cuyo logaritmo se aproximaba más a la expresión ln a + ln b. La hoy desaparecida regla de cálculo utilizaba el mismo proceso.

Prueba: Sea f(x) = ln (ax) - ln x. Derivando: f'(x) = a·(1/ax) - 1/x = 1/x - 1/x = 0, lo que significa que f es constante en el intervalo (0, + ∞). En consecuencia f(b) = f(1), es decir: ln ab - ln b = ln a -ln 1, o sea ln ab = ln a + ln b.

Consecuencias:

ln (1/a) = - ln a. (2)

En efecto, ln(a) + ln (1/a) = ln (a· 1/a) = ln 1 = 0.

ln (a/b) = ln a - ln b. (3)

En efecto ln (a/b) = ln (a·1/b) = ln a + ln (1/b) = ln a - ln b.

ln (aⁿ) = n.ln a. (4) , para cualquier valor real de n.

Esto se demuestra por inducción para todo número entero natural "n", y luego para todo "n" entero, con (2), y luego para todo "n" racional, utilizando (3). La continuidad del logaritmo hace que una relación cierta en los racionales es también válida en los reales, lo que acaba la prueba.

Esta última relación permite resolver ciertas ecuaciones con la incógnita en el lugar de las potencias: a^x = b tiene como solución x = lnb/lna cuando a ≠ 1, a>0 y b>0.

... / geometria