Composición de funciones
Dadas dos funciones 
y 
tales que la imagen de 
está contenida en el dominio de 
, se define la función composición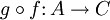 
como el conjunto de pares 
, para todos los elementos 
de 
.
Dado conocemos 
, puesto que conocemos la función , y dado cualquier elemento 
de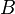 
conocemos también 
, puesto que conocemos la función . Por tanto,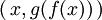 
está definido para todo x. Luego 
cumple la condición de existencia que se exige a las funciones.
También cumple la condición de unicidad, dado que para cada el valor de 
es único, y para cada también lo es el de 
, por ser 
y 
funciones.
La composición de funciones es asociativa:
Sin embargo, en general, la composición de funciones no es conmutativa. Dadas 
y 
, 
puede no tener ni siquiera sentido, porque “devuelve” elementos de 
, en tanto que está definida en el dominio . Pero incluso en los casos en que dominios y codominios son compatibles (o son el mismo conjunto), nada garantiza que la composición de funciones sea conmutativa. Por ejemplo, con funciones numéricas 
y 
, 
, en tanto que 
... limites
No hay comentarios:
Publicar un comentario