Distancia

La distancia es una magnitud escalar que mide la relación de lejanía entre dos puntos.

En el espacio euclídeo la distancia entre dos puntos coincide con la longitud del camino más corto entre dos puntos, sin embargo, eso no nos sirve como definición formal de distancia, ya que para la definición de longitud es necesaria la de la distancia. Por eso en este artículo se acude a una definición formal de distancia. Además en espacios de geometrías más complejas el concepto de distancia y el de longitud de una curva no tienen porqué coincidir.

Definición formal

Desde un punto de vista formal, para un conjunto de elementos X se define distancia o métrica como cualquier función binaria d(a,b) de 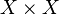en que verifique las siguientes condiciones:

• No negatividad:
• Simetricidad:
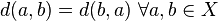
• Desigualdad triangular:
• .
• Si 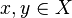son tales que d(x,y) = 0, entonces x = y.

Distancia (geometría)

Se denomina distancia euclídea entre dos puntos A(x₁,y₁) y B(x₂,y₂) del plano a la longitud del segmento de recta que tiene por extremos A y B. Puede calcularse así:

La distancia entre un punto P y una recta R es la longitud del segmento de recta que es perpendicular a la recta R:Ax + By + C = 0 y la une al punto P(x₁,y₁). Puede calcularse así:

donde |·| denota valor absoluto.

La distancia entre dos rectas paralelas es la longitud del segmento de recta perpendicular a ambas que las une.

La distancia entre un punto P y un plano L es la longitud del segmento de recta perpendicular al plano L = Ax + By + Cz + D que lo une al punto P(x₁,y₁,z₁) y puede calcularse así:

... Inecuaciones

logaritmos

Logaritmo

En Matemática, el logaritmo es la función inversa de la función potencia x = bⁿ, que permite obtener n. Esta función se escribe como n = log_b x. Es el exponente o potencia a la que un número fijo, llamado base, se ha de elevar para dar un número dado. Por ejemplo, en la expresión 10² = 100, el logaritmo de 100 en base 10 es 2. Esto se escribe como log₁₀ 100 = 2.

Por ejemplo:

3⁴ = 81

El logaritmo es una de tres funciones relacionadas entre sí: en bⁿ = x, b puede ser encontrado con radicales, n con logaritmos y x con exponenciación. Se denomina logaritmo neperiano o logaritmo natural (ln) al logaritmo en base e de un número.

Logaritmos en otras bases

La elección de un determinado número como base de los logaritmos no es crucial, debido a que se pueden hacer conversiones de una base a otra de forma sencilla. Para ello, es útil la siguiente fórmula que define al logaritmo de x en base b (suponiendo que b, x, y k son números reales positivos y que tanto "b" como "k" son diferentes de 1):

en la que "k" es cualquier base válida. Si hacemos k=x, obtendremos:

En la práctica, se emplea el logaritmo decimal, que se indica como , en ciencias que hacen uso de las matemáticas, como la química en la medida de la acidez (denominada pH) y en física en magnitudes como la medida de la luminosidad (candela), del sonido(dB), de la energía de un terremoto (escala de Richter), etc. En informática se usa el logaritmo en base 2 la mayoría de veces. Las propiedades de los logaritmos son una base que facilita aún más su resolución.

Propiedad fundamental

La denominada propiedad fundamental, definida por:

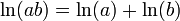(1) (con a>0 y b>0)

fue la que permitió construir las primeras tablas de logaritmos, cuyo propósito era hacer que calcular un producto fuese tan rápido como hallar una suma. En efecto, para calcular un producto se buscaban en la tabla los logaritmos de los factores, se sumaban, y se buscaba el número cuyo logaritmo se aproximaba más a la expresión ln a + ln b. La hoy desaparecida regla de cálculo utilizaba el mismo proceso.

Prueba: Sea f(x) = ln (ax) - ln x. Derivando: f'(x) = a·(1/ax) - 1/x = 1/x - 1/x = 0, lo que significa que f es constante en el intervalo (0, + ∞). En consecuencia f(b) = f(1), es decir: ln ab - ln b = ln a -ln 1, o sea ln ab = ln a + ln b.

Consecuencias:

ln (1/a) = - ln a. (2)

En efecto, ln(a) + ln (1/a) = ln (a· 1/a) = ln 1 = 0.

ln (a/b) = ln a - ln b. (3)

En efecto ln (a/b) = ln (a·1/b) = ln a + ln (1/b) = ln a - ln b.

ln (aⁿ) = n.ln a. (4) , para cualquier valor real de n.

Esto se demuestra por inducción para todo número entero natural "n", y luego para todo "n" entero, con (2), y luego para todo "n" racional, utilizando (3). La continuidad del logaritmo hace que una relación cierta en los racionales es también válida en los reales, lo que acaba la prueba.

Esta última relación permite resolver ciertas ecuaciones con la incógnita en el lugar de las potencias: a^x = b tiene como solución x = lnb/lna cuando a ≠ 1, a>0 y b>0.

... / geometria