Geometría
La geometría es una rama de la matemática que estudia representaciones del espacio: puntos, rectas, planos, polígonos, poliedros, curvas, superficies, etc. Se utiliza para solucionar problemas concretos y es la justificación teórica de muchos instrumentos: compás, teodolito, pantógrafo, etc. Una parte importante de la geometría clásica es el estudio de las construcciones con regla y compás.También da fundamento teórico a inventos como el sistema de posicionamiento global (en especial cuando se la considera en combinación con el Análisis Matemático y sobre todo con las Ecuaciones diferenciales). Es útil en la preparación de diseños (justificación teórica de la Geometría Descriptiva y del Dibujo Técnico), e incluso en la fabricación de artesanías.
Las figuras geométricas y las construcciones
Una figura geométrica es, en la geometría euclidiana, todo espacio encerrado entre líneas. Las construcciones son secuencias de operaciones elementales para construir estas figuras geométricas.
En Geometría Clásica solo se buscaban construcciones con regla y compás. Las construcciones son equivalentes al concepto de algoritmo en una álgebra.
La geometría ha sido desde los principios de la humanidad un mecanismo utilizado para encontrar soluciones a los problemas más comunes de quienes la han aplicado en su vida, pues, entre otros usos, facilita la medición de estructuras sólidas reales, tanto tridimensionales como superficies planas y además es bastante útil para la realización de complejas operaciones matemáticas.
El avance de la geometría depende fuertemente del avance en las definiciones; las propiedades de los triángulos son posibles de enunciar sin hacer referencia a éstos, pero sería un proceso largo, tedioso e inútil. Por lo tanto, los teoremas relativos a cada figura que se defina (y su respectiva definición), serán enunciados dentro de sus páginas respectivas.
- Las figuras fundamentales (sin definición): punto, recta y plano.
- En la recta se pueden ver: segmentos, semirrectas y vectores.
- En el plano, una recta determina dos semiplanos; su intersección determina las figuras convexas: faja, ángulo, triángulo, cuadriángulo y polígono.
- Utilizando el concepto de distancia, se definen: el círculo y la esfera.
- Utilizando el concepto de semiespacio se definen: el diedro, el espacio prismático, el triedro, el ángulo poliedro y los poliedros. Entre los últimos encontramos como casos particulares: el tetraedro, el prisma, la pirámide y el paralelepípedo.
- El concepto de círculo en el espacio da origen a: el cono y el cilindro.
Existen otras figuras geométricas, que serán definidas dentro de cada página vinculada a ésta.
Geometría analítica
Se conoce como Geometría Analítica al estudio de ciertos objetos geométricos mediante técnicas básicas del Análisis Matemático y del Álgebra. Se podría decir que es el desarrollo histórico que comienza con la Geometría Cartesiana y concluye con la aparición de la Geometría Diferencial con Gauss y más tarde con el desarrollo de la Geometría Algebraica.
Lo novedoso de la Geometría Analítica es que permite representar figuras geométricas mediante fórmulas del tipo f(x,y) = 0, donde f representa una función. En particular, las rectas pueden expresarse como ecuaciones polinómicas de grado 1 (v.g.: 2x + 6y = 0) y las circunferencias y el resto de cónicas como ecuaciones polinómicas de grado 2 (v.g.: la circunferencia x2 + y2 = 4, la hipérbola xy = 1 ).
Construcciones fundamentales.
En un sistema de coordenadas cartesianas, un punto del plano queda determinado por dos números, que son la abscisa y la ordenada del punto, de forma que, a todo punto del plano corresponden siempre dos números reales ordenados (abscisa y ordenada), y recíprocamente, a un par ordenado de números corresponde un único punto del plano.
Consecuentemente el sistema cartesiano establece una correspondencia biunívoca entre un concepto geométrico como es el de los puntos del plano y un concepto algebraico como son los pares ordenados de números. Esta correspondencia constituye el fundamento de la Geometría Analítica.
Con la Geometría Analítica se puede determinar figuras geométricas planas por medio de ecuaciones e inecuaciones con dos incógnitas. Este es un método alternativo de resolución de problemas, o cuando menos nos proporciona un nuevo punto de vista con el cual poder atacar el problema.
Localización de un punto en el Plano Cartesiano.
En un plano traza dos rectas perpendiculares (ejes) —que por convenio se trazan de manera que una de ellas sea horizontal y la otra vertical—, y cada punto del plano queda unívocamente determinado por las distancias de dicho punto a cada uno de los ejes, siempre y cuando se dé también un criterio para determinar sobre qué semiplano determinado por cada una de las rectas hay que tomar esa distancia, criterio que viene dado por un signo. Ese par de números, las coordenadas, quedará representado por un par ordenado (x,y), siendo x la distancia a uno de los ejes (por convenio será la distancia al eje vertical) e y la distancia al otro eje (al horizontal).
En la coordenada x, el signo positivo (que suele omitirse) significa que la distancia se toma hacia la derecha del eje vertical (eje de ordenadas), y el signo negativo (nunca se omite) indica que la distancia se toma hacia la izquierda. Para la coordenada y, el signo positivo (también se suele omitir) indica que la distancia se toma hacia arriba del eje horizontal (eje de abscisas), tomándose hacia abajo si el signo es negativo (tampoco se omite nunca en este caso). A la coordenada x se la suele denominar abscisa del punto, mientras que a la y se la denomina ordenada del punto.
Los puntos del eje de abscisas tiene por lo tanto ordenada igual a 0, así que serán de la forma (x,0), mientras que los del eje de ordenadas tendrán abscisa igual a 0, por lo que serán de la forma (0,y).
El punto donde ambos ejes se cruzan tendrá por lo tanto distancia 0 a cada uno de los ejes, luego su abscisa será 0 y su ordenada también será 0. A este punto —el (0,0)— se le denomina origen de coordenadas.
Ecuaciones de la recta en el plano.
Una recta en el plano se representa con la Función lineal de la forma:
como expresión general, si bien podemos distinguir dos casos particulares. Si una recta no corta a uno de los ejes, será porque es paralela a él. Como los dos ejes son perpendiculares, si no corta a uno de ellos forzosamente ha de cortar al otro. Tenemos pues dos casos:
Rectas que no cortan al eje de las ordenadas.
Estas rectas son, entonces, paralelas a dicho eje. Se denominan rectas verticales. El punto de corte de una de dichas rectas con el eje de las abscisas será entonces el punto (x0,0). La ecuación de dicha recta es, por lo tanto es:
Rectas que no cortan al eje de las abscisas.
Estas rectas son entonces paralelas a dicho eje. Se denominan rectas horizontales. El punto de corte de una de dichas rectas con el eje de las ordenadas será entonces el punto (0,y0). La ecuación de dicha recta es, por lo tanto:
Rectas oblicuas.
Cualquier otro tipo de recta recibe el nombre de recta oblicua. En ellas hay un punto de corte con el eje de abscisas (a,0) y otro punto de corte con el eje de ordenadas (0,b). El valor a recibe el nombre de abscisa en el origen, mientras que el b se denomina ordenada en el origen.
Cónicas.
Así, por ejemplo, la geometría analítica plana describe una elipse, centrada en el origen de un sistema de coordenadas cartesianas con la siguiente expresión:
donde a y b son constantes que se identifican como los semiejes mayor y menor de la elipse.
Un caso especial de estas curvas cónicas es la circunferencia, lo cual es una cónica donde a = b.
Circunferencia
En matemática, una circunferencia (del latín circunferentia) es una curva plana cerrada cuyos puntos son equidistantes de un punto interior fijo llamado centro. Cabe aquí hacer la distinción entre circunferencia y círculo: la primera es solo el contorno externo y el segundo incluye también toda el área interior.
Es la curva de máxima simetría bidimensional y sus aplicaciones son tan numerosas (saltan a la vista) que sería ocioso (poco productivo) hacer un recuento de ellas.
En geometría analítica, la ecuación --en coordenadas cartesianas-- de una circunferencia centrada en el punto (h, k) y de radio r, es:
Desarrollando la ecuación, se tiene:
siendo  ;
;  y
y 
La longitud de una circunferencia es:
donde r = radio y π (el número pi) es el cociente entre el diámetro y la longitud de la circunferencia.
Ecuación en coordenadas cartesianas
En un sistema de coordenadas cartesianas x-y, la circunferencia con centro en el punto (a, b) y radio c consta de todos los puntos (x, y) que satisfacen la ecuación
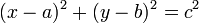 .
.
Cuando el centro está en el origen (0, 0), la ecuación anterior se simplifica a
La circunferencia con centro en el origen y de radio igual a 1 es llamada circunferencia unidad (o circunferencia unitaria).
Si en vez del centro y el radio son dados dos puntos (x1,y1),(x2,y2) extremos de un diámetro, la circunferencia queda descrita por la ecuación
Ecuación en coordenadas polares
Cuando la circunferencia tiene centro en el origen y el radio es c, se describe en coordenadas polares como (r,θ)
Cuando el centro no está en el origen sino en el punto (s,α) y el radio es c, la ecuación se convierte en
Existen varias rectas y puntos especiales en la circunferencia. Un segmento que une dos puntos de la circunferencia se llama cuerda. A las cuerdas de longitud máxima (aquellas que pasan por el centro) se les llama diámetros. Se conoce como radio del círculo a cualquier segmento que une el centro con la circunferencia, así como a la longitud de los mismos.
Una línea que atraviesa la circunferencia, cortándolo en dos puntos, se llama secante, mientras que una línea que toca a la circunferencia en un sólo punto se denomina tangente. El punto de contacto de la tangente con la circunferencia se llama punto de tangencia. El radio que une el centro con el punto de tangencia es perpendicular a la tangente.
Área del círculo
El área del círculo delimitado por la circunferencia es:
Esta última fórmula se debe a que, sabiendo que el área de cualquier polígono regular es igual al producto del apotema y el perímetro del polígono dividido entre 2, es decir: 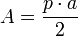 . Y aproximando la circunferencia como el límite de polígonos regulares, entonces el apotema coincide con el radio de la circunferencia, y el perímetro con la longitud, por tanto:
. Y aproximando la circunferencia como el límite de polígonos regulares, entonces el apotema coincide con el radio de la circunferencia, y el perímetro con la longitud, por tanto:




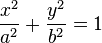

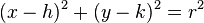
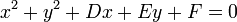





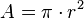
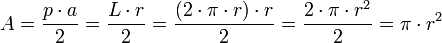
No hay comentarios:
Publicar un comentario