Distancia
La distancia es una magnitud escalar que mide la relación de lejanía entre dos puntos.
En el espacio euclídeo la distancia entre dos puntos coincide con la longitud del camino más corto entre dos puntos, sin embargo, eso no nos sirve como definición formal de distancia, ya que para la definición de longitud es necesaria la de la distancia. Por eso en este artículo se acude a una definición formal de distancia. Además en espacios de geometrías más complejas el concepto de distancia y el de longitud de una curva no tienen porqué coincidir.
Definición formal
Desde un punto de vista formal, para un conjunto de elementos X se define distancia o métrica como cualquier función binaria d(a,b) de  en
en  que verifique las siguientes condiciones:
que verifique las siguientes condiciones:
- No negatividad:

- Simetricidad:
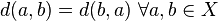
- Desigualdad triangular:

 .
.- Si
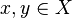 son tales que d(x,y) = 0, entonces x = y.
son tales que d(x,y) = 0, entonces x = y.
Distancia (geometría)
Se denomina distancia euclídea entre dos puntos A(x1,y1) y B(x2,y2) del plano a la longitud del segmento de recta que tiene por extremos A y B. Puede calcularse así:
La distancia entre un punto P y una recta R es la longitud del segmento de recta que es perpendicular a la recta R:Ax + By + C = 0 y la une al punto P(x1,y1). Puede calcularse así:
donde |·| denota valor absoluto.
La distancia entre dos rectas paralelas es la longitud del segmento de recta perpendicular a ambas que las une.
La distancia entre un punto P y un plano L es la longitud del segmento de recta perpendicular al plano L = Ax + By + Cz + D que lo une al punto P(x1,y1,z1) y puede calcularse así:



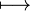



 , en ciencias que hacen uso de las matemáticas, como la química en la medida de la acidez (denominada
, en ciencias que hacen uso de las matemáticas, como la química en la medida de la acidez (denominada 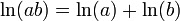 (1) (con a>0 y b>0)
(1) (con a>0 y b>0)

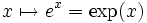

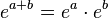
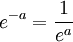

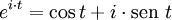 .
.


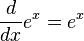
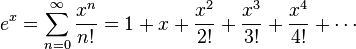

![f: R \rarr Z / f(x) = [x] = ent(x)](http://upload.wikimedia.org/math/7/1/1/7110a1c26b35e525f4b8a7b8a3e10921.png) está definida por:
está definida por:

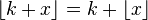


 donde
donde 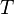 es el
es el  . Estas últimas también son conocidas como funciones simétricas de media onda y constan de dos semiondas iguales de sentidos opuestos
. Estas últimas también son conocidas como funciones simétricas de media onda y constan de dos semiondas iguales de sentidos opuestos![[a,b] \harr \forall x_1, x_2 \in [a,b]: x_1 < x_2 \harr f(x_1) < f(x_2)](http://upload.wikimedia.org/math/3/d/9/3d9b9a35a4fb0bf3964d20ceadd066f3.png)
![[a,b] \harr \forall x_1, x_2 \in [a,b]: x_1 < x_2 \harr f(x_1) > f(x_2)](http://upload.wikimedia.org/math/8/4/9/849a82a7a504c0a8212339b59a9ed44f.png)
![[a,b] \harr \forall x_1, x_2 \in [a,b]: x_1 < x_2 \harr f(x_1) \le f(x_2)](http://upload.wikimedia.org/math/e/e/6/ee6895604b23a297a82b7f5423ce0214.png)
![[a,b] \harr \forall x_1, x_2 \in [a,b]: x_1 < x_2 \harr f(x_1) \ge f(x_2)](http://upload.wikimedia.org/math/b/b/c/bbc686dc99b37b9798c8fbdc5f5173ad.png)